Размещение элементов СИБ в АИС
И.Б.Шнайдерман, С.А.Охрименко, Г.А.Черней
Представляется возможным исследование оценки эффективности и размещения элементов СИБ в автоматизированных информационных (государственных и коммерческих) системах [3]. В качестве основных характеристик используем производительность и стоимость СИБ [1, 6]. При отсутствии механизмов защиты нарушителю не требуются серьезные усилия для получения доступа. В АИС со слабой защитой усилия нарушителя пропорциональны затратам на обеспечение безопасности. Системы с высоким уровнем защиты характеризуются тем, что незначительные усилия по обеспечению безопасности приводят к существенному повышению затрат нарушителя для получения несанкционированного доступа. В условиях создания идеальной системы защиты [2], что является достижимым только при высоких затратах, нарушитель несет непомерно высокие затраты для преодоления механизмов СИБ.
При решении задачи могут быть использованы следующие подходы: динамическое программирование; смешанное целочисленное линейное программирование; эвристические методы [4, 5].
При использовании динамического программирования АИС представляется в виде дерева узлов, соединенных ориентированными дугами. Решение проблемы размещения и оценки СИБ в узлах АИС формулируется следующим образом: стоит ли устанавливать состветствующий тип СИБ (или несколько типов одновременно) в каждом узле, и если стоит, то какого типа требуется установить. В качестве исходных данных используем следующие:
di - запрос (сообщение), поступающий в узел сети;
p1,p2,p1,2 - стоимость установки СИБ первого типа, второго типа и обоих типов одновременно;
![]() -
коэффициенты стоимости передачи запроса
(сообщения) для СИБ первого и второго типов (
-
коэффициенты стоимости передачи запроса
(сообщения) для СИБ первого и второго типов (![]() r>1);
r>1);
cij - стоимость передачи одного запроса (сообщения), необработанного в плане СИБ, по линии (i,j);
bij - стоимость передачи одного запроса (сообщения), обработанного в плане СИБ, по линии (i,j);
pi - стоимость передачи одного блока обработанных данных из узла i в следующую точку;
q1,q2 - приращение стоимости для СИБ первого и второго типов;
Ri - множество узлов, непосредственно связанных с узлом i;
s(i) - узел, следующий за узлом i;
s2(i) = s(s(i)); sm(i) - узел, следующий за узлом через (m-1) узел;
bilm - стоимость передачи блока данных, поступающих в узел i из узла s(i);
Значения b вычисляются с использованием следующих рекурсивных соотношений:
для j=s(i) и k=s(i)
bi11=pi
bilm=bjk+bi l m-1 для m>2 (1)
bilm=cik+bi l-1 m-1 для m>l>2
и если N - выбранная точка сети и iОRN, то bi11=0.
После этого имеется возможность определения лучшего варианта размещения СИБ (по критерию стоимости, с условием обеспечения требуемой надежности) для поддерева с корнем в узле i :
min{Z0,Z1,Z2,Z3} (2)
где Z - стоимость четырех вариантов СИБ для сети (Z0 - СИБ отсутствует и заменена внешним организационно-техническим контуром, Z1- только СИБ первого типа, Z2 - СИБ второго типа, Z3 - СИБ обоих типов).
Введем следующие дополнительные условные обозначения:
film - стоимость варанта СИБ для всего трафика, входящего в узел i, при условии, что первый тип СИБ, через который пройдет поток данных после узла i, встретится в узле sl(i), а второй тип СИБ в узле sl(i) или sm(i) при условии, что 1 < l < m;
qilmv - стоимость варианта для всего трафика, входящего в узел i, при условии, что первый тип СИБ, через который пройдет поток данных после узла i, встретится в узле sl(i), второй тип СИБ в узле sm(i), а следующийвторой тип СИБ в узле sl(i) или sv(i) при условии, что 1<m<l<v.
Тогда для j=s(i) и l < m, получаем:
![]()
![]() ; (3)
; (3)
![]() для всех
l;
для всех
l;
![]() ;
;
![]() ; для
всех l и m;
; для
всех l и m;
для j=s(i) и m < l < v получаем:
![]() (4)
(4)
где Y определяется аналогично Z.
При использовании смешанного целочисленного программирования отпадает необходимость в предварительном определении деревьев для каждого узла и считается, что данные могут передаваться в любом направлении. Для данного случая необходимо минимизировать стоимостную функцию, учитывающую размещение типов системы ИБ.
При использовании эвристических алгоритмов задача формулируется следующим образом: необходим выбор минимальной по стоимости СИБ, обеспечивающей прохождение от выбранной точки i сети к рассматриваемому узлу, при обеспечении требуемого уровня надежности. Для данного случая минимальное по стоимости решение d(z) из заданного множества типов СИБ может быть получено из следующего уравнения:
![]() (5)
(5)
где ![]() -
стоимость минимального трафика из узла i к
следующей точке сети для множества типов системы
ИБ.
-
стоимость минимального трафика из узла i к
следующей точке сети для множества типов системы
ИБ.
Выбор конфигурации системы ИБ для АИС может быть осуществлен на основе итераций путем исключения конкретного типа СИБ без снижения общего уровня надежности. Для описания алгоритма выбора конфигурации введем следующие обозначения:
![]() -
множество типов СИБ для итерации t;
-
множество типов СИБ для итерации t;
![]() - новое
множество типов системы ИБ, полученное путем
исключения конкретного типа СИБ
- новое
множество типов системы ИБ, полученное путем
исключения конкретного типа СИБ ![]() в узле i уровня m
сети.
в узле i уровня m
сети.
Итерационный процесс может быть описан следующим образом:
Шаг 1: Пробное исключение одного из типов СИБ из zt .
Для каждого pim такого, что ztim=1
вычисляется ci(ztim) -
общая минимальная стоимость трафика при наличии
множества типов СИБ ![]() .
.
Шаг 2: Для исключения типа СИБ определяется:
![]() (7)
(7)
Если ![]() , то
алгоритм прекращает работу, поскольку
дальнейшее уменьшение стоимости (при сохранении
требуемого уровня надежности) невозможно. В
противном случае тип системы ИБ исключается:
, то
алгоритм прекращает работу, поскольку
дальнейшее уменьшение стоимости (при сохранении
требуемого уровня надежности) невозможно. В
противном случае тип системы ИБ исключается:
![]() (8)
(8)
![]() при t=t+1
при t=t+1
Переход к шагу 1.
Решение данной задачи может быть выполнено также с помощью гибридного метода, объединяющего имитационные и аналитические модели. К числу преимуществ данного подхода можно отнести: существенное уменьшение сложности модели; возможность обнаружения критических элементов; повышение чувствительности модели к внешним и внутренним возмущениям; простота реализации и др.
Введем следующие дополнительные условные обозначения. Пусть АИС состоит из M компонентов (N - узлов и L коммуникационных линий), причем M=N+L. Стохастический процесс X(t)=(X1(t),...,XM(t)) oпределяет функциональный статус сетевых компонент следующим образом:
м1, если компонента находится в работоспособном
Xk(t) = нсостоянии в момент времени t ;
о0, в противном случае, для k=1,...,M.
Область состояний АИС ![]() содержит 2M
различных состояний. Пусть p(x) определяет
вероятность устойчивого состояния для тех
случаев, когда глобальное состояние АИС равно x.
Для глобального состояния x характеристики
АИС определяются следующим процессом:
содержит 2M
различных состояний. Пусть p(x) определяет
вероятность устойчивого состояния для тех
случаев, когда глобальное состояние АИС равно x.
Для глобального состояния x характеристики
АИС определяются следующим процессом:
Y(x)=(Y1(x),...,YM(x)) (9)
область состояний которого равна ![]() .
.
Для характеристики устойчивого
состояния АИС с точки зрения СИБ может
использоваться достаточное количество
показателей, в их числе такие, как средняя
задержка данных, среднее время вызова узла,
вероятность блокировки и многие др. Процесс
считается устойчивым, если в АИС при
возникновении отказа или изменении глобального
состояния, поток данных переходит в состояние
равновесия. Это означает, что при изменении
состояния АИС (например, из x в x’)
устойчивое состояние Y(x) переходит в
устойчивое состояние Y(x’) без отклонения. В
свою очередь, область ![]() , может быть разделена на два следующих
подмножества:
, может быть разделена на два следующих
подмножества:
- подмножество S, характеризующее допустимое состояние АИС с сохранением функциональных характеристик;
- подмножество F ![]() , характеризующее состояние АИС с
характеристиками ниже допустимого.
, характеризующее состояние АИС с
характеристиками ниже допустимого.
Как отмечалось выше, для характеристики состояния АИС может использоваться множество показателей. Их можно представить в виде вектора показателей эффективности. Один из возможных вероятностных показателей может быть определен следующим образом:
![]() (10)
(10)
В свою очередь, средняя характеристика i-го компонента вектора показателей эффективности Y(x) рассчитывается следующим образом:
![]() i=1,...,n.
(11)
i=1,...,n.
(11)
Множество состояний, характеризующих
множества ![]() и
и ![]() , могут включать
достаточно большое их количество, что делает
практически невозможным расчет полной суммы. Для
исключения подобного необходимо ограничить
расчет суммы только в выбранных точках (например,
в точке x), которая выбирается на основе
следующего условия:
, могут включать
достаточно большое их количество, что делает
практически невозможным расчет полной суммы. Для
исключения подобного необходимо ограничить
расчет суммы только в выбранных точках (например,
в точке x), которая выбирается на основе
следующего условия:
![]() (12)
(12)
где b- бесконечно малое число.
В свою очередь, среднюю характеристику i-го компонента вектора показателей эффективности можно представить следующим образом:
![]() (13)
(13)
где ![]() . .
. .
Применительно к данному выражению представляется возможным объединение имитационного моделирования по методу Монте-Карло с аналитической моделью в следующей последовательности итерационных операций.
Шаг 1. С помощью имитационной
модели получают состояние xi из
множества ![]() в
соответствии с распределением вероятности p(x).
в
соответствии с распределением вероятности p(x).
Шаг 2. На основе рассчитанного, с использованием аналитических зависимостей состояния xi определяются следующие показатели:
![]()
![]() для j=1,...,m
(14)
для j=1,...,m
(14)
Шаг 3. После n повторов вычислений приведенных показателей оценивается общий коэффициент готовности по следующей формуле:
![]() (15)
(15)
и значение среднего j-го компонента показателя эффективности
![]() для j=1,...,m
(16)
для j=1,...,m
(16)
Функция вероятности p(x) рассчитывается как
![]() (17)
(17)
где pk=p {компонент k исправен и обеспечивает требуемый уровень надежности} при k=1,...,M. Для тех случаев, когда отмечаются зависимые друг от друга отказы и сбои, вызванные неисправностями и срывами компонент системы ИБ, состояние сети генерируется с помощью следующих итераций.
Шаг 1. Определяется вектор x=(x1,...,xM) с использованием распределения, приведенного в (17).
Шаг 2. Если s(k) определяет множество соседних с k-м компонентом системы ИБ и на первом этапе x=0, то для всех jОS(k) рассчитывается состояние в соответствии со следующим распределением:
p{xj=1} = 1 - p{xj = pj/2} (18)
Другими словами, на первом этапе генерируются возможные отказы компонент системы ИБ сети с вероятностью p(x). На втором этапе генерируются отказы только тех узлов, которые соединены с отказавшими компонентами СИБ на первом этапе.
Для оценки функционирования АИС с точки зрения безопасности можно использовать также показатель Cg=p{все узлы сети доступны}, то есть
м1, если все узлы доступны;
Yj(x)= н
о0, в противном случае.
Возможно использование и другого показателя - вероятности того, что узел j доступен всем узлам, включенным в множество s(i), то есть
м1, если узел j доступен всем узлам ![]() ;
;
Cj,s(j)(x)= н
о0, в противном случае.
С целью оптимизации характеристик АИС можно получить также информацию о чувствительности системы к изменению СИБ, используя метод малого периметра. С этой целью запишем общий показатель эффективности сети в виде следующего выражения:
![]() (19)
(19)
Соответственно компоненты будут определены как
![]() , i=1,...,m
(20)
, i=1,...,m
(20)
В данном случае функция вероятности
может зависеть от значения вектора параметров ![]() , где
, где ![]() Q (через Q обозначим
множество допустимых значений
Q (через Q обозначим
множество допустимых значений ![]() ). Тогда (19 и 20) примут следующий вид
). Тогда (19 и 20) примут следующий вид
![]() (21)
(21)
![]() , i=1,...,m (22)
, i=1,...,m (22)
Следующей задачей является оптимизация размещения элементов СИБ по критериям ценности информации, содержащейся в конкретном узле АИС, а также уязвимости соответствующего узла по отношению к группам программных злоупотреблений. Рассмотрим практическую реализацию рассмотренных задач. На рис.1 приведена топология гипотетической АИС, на основе которой построена матрица взаимосвязей СИБ (таб.1). Реализация рассматриваемых моделей оценки эффективности и размещения элементов СИБ позволяет получить схему размещения (табл.2.) с условием сохранения необходимого уровня надежности.
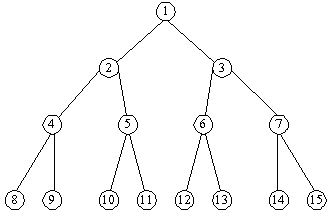
Рис. 1 Архитектура гипотетической АИС.
Таблица 1
Матрица взаимосвязей узлов гипотетической АИС
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
6 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
7 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
8 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
11 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
12 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
13 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
14 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
15 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Таблица 2
Размещение СИБ в узлах гипотетической АИС
Узел |
Тип СИБ |
1 |
2 |
2 |
1 |
3 |
1 |
4 |
0 |
5 |
0 |
6 |
0 |
7 |
0 |
8 |
3 |
9 |
3 |
10 |
3 |
11 |
3 |
12 |
3 |
13 |
3 |
14 |
3 |
15 |
3 |
Необходимо решение дополнительной задачи размещения элементов СИБ по критерию стоимости. В качестве целевой функции задается стоимость СИБ и с помощью последовательных итерационных операций расчета показателей эффективности определяют максимальный уровень надежности с учетом степени риска нарушения целостности.
Приведенный комплекс алгоритмов может служить основой для оценки эффективности и размещения системы информационной безопасности.
Описаный подход позволяет разместить СИБ с условием сохранения необходимого уровня надежности. Но может возникнуть ситуация, когда в сети размещается СИБ с заданными показателями стоимости. Для решения данной задачи задавают функцию стоимости, и методом перестановок и пересчетом показателей эффективности получают максимальный уровень надежности от размещения СИБ в сети. Непосредственным образом с уровнем надежности связана степень риска нарушения целостности компьютерной системы.
В качестве показателя оценки степени риска могут использоваться показатель ожидаемых потерь:
![]() (23)
(23)
где ![]() (24)
(24)
Ki(AjZjk) - показатель, характеризующий ожидаемые потери от хищения информации Aj из узла i, при нарушении целостности СИБ вида k в i-м узле (k = 0;1;2;1,2);
Mi(Aj) - максимальный уровень потерь от хищения нарушителем информации Aj из узла i;
P(Zk) - вероятность преодоления нарушителем k-го типа СИБ;
В заключении следует отметить, что размещение и использование СИБ в системе можно считать эффективным только в случае, если при известной степени риска, затраты злоумышленника на нарушение целостности АИС будут больше чем выигрыш, полученный от использовании полученной информации.
ЛИТЕРАТУРА.
- Бияшев Р.Г., Афонская Т.Л. Некоторые задачи защиты информации. //Зарубежная радиоэлектроника.-1994, №2-3, с.42-45.
- Сюнтюренко О.В. Формирование норм защищенности на основе модели идеальной защиты.//Зарубежная радиоэлектроника. -1993, №7-9, с.92-96.
- Barker L., Nelson l., Security standarts - government and commercial.//AT&T Technic Journal. -1988, vol.67,№3, p.9-18.
- Grimm R. Security on networks: do we realy need it? //Computer networks and ISDN Systems.-1989, vol.17, №10, p.315-323.
- Helme M., Jack C., Shulman A. Planning for new services in the local loop.// Teletraffic science in new cost-eff. Systems, networks and services. Amsterdam, 1989, p.461-472.
- Hindes S. Computer security and control principles.//Computer-Audit Update. -1993 (september), p.11-12.